Contents of this page may be automatically translated, we take no responsibility for the accuracy of the translation. Feel free to contact our customer support centre if you have any questions.

The distance to a satellite is measured by determining how many whole wavelengths plus a last part of a wavelength there are between the satellite and the receiver. Carrier phase measurement provides the opportunity for a more accurate distance measurement than code measurement. However, carrier phase measurement is more complicated than code measurement because the signal's carrier phase has no time markers.
The principle of carrier phase measurement
The distance between satellite and receiver in carrier phase measurement can in principle be expressed as several whole wavelengths plus a part of the last wavelength (see picture below). Part of the last wavelength is determined accurately by phase measurement, but the number of whole wavelengths will initially be unknown.
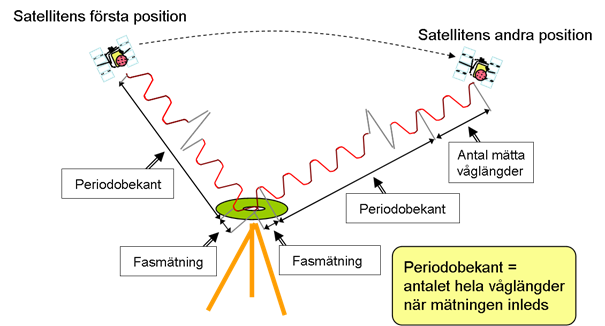
Determination of the number of whole wavelengths
The number of whole wavelengths that the distance between satellite and receiver consists of at the start of the measurement is called ambiguity. Proper determination of ambiguity is very critical for accurate positioning. If, for example, the ambiguity is mis-determined to adjacent integers, this means that the searched distance between satellite and receiver is 19 centimetres too long or short!
The determination of integer ambiguities is facilitated by:
- relative positioning, which reduces sources of error
- multi-frequency measurement
- good mathematical models
- combination with code measurement, which provides the opportunity to limit or "circle" the number of possible integer phase ambiguities.
In connection with real-time measurement, it is desired to combine these factors in various ways to minimize the time from the start of measurement until the so-called fix solution has been reached, i.e., when the ambiguity has been determined ("fixed"). This process is called initialization and requires the GNSS receiver to maintain lock-on to the signal from the time you start the phase measurement. Temporary interruptions result in an unknown number of periods being lost in the measurement, so-called cycle slips. If it is not possible to correct the cycle slips with the appropriate method, the initialization of the phase measurement must be started again.
Description of the carrier phase signal
The carrier phase of L1 has a much higher frequency than the C/A code, 1575 MHz, which corresponds to a wavelength of 19 centimetres. Based on the rule of thumb that the signal resolution is about one percent of the wavelength, you can in principle make a single carrier phase measurement with an accuracy of about two millimetres!
Why, then, isn't all measurement done with a carrier phase if it is so much more accurate than code measurement? The simple answer is that carrier phase measurement is more complicated, both in terms of equipment and measurement method.
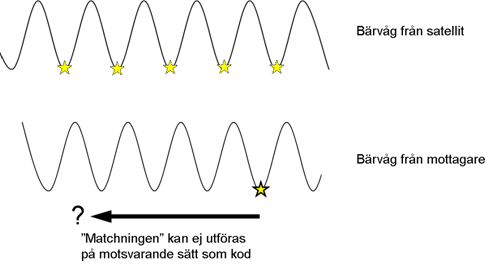
The encoded signal, such as the C/A code for GPS, is intentionally designed to facilitate signal matching and timing. The carrier phase, on the other hand, has no time markers at all, since each full wavelength or period in the carrier phase is the same as the other (see picture above; in reality, however, the satellite signal is Doppler shifted).

