Basics of map projections

Mapping of the curved surface of the earth - or actually the earth model, which is an ellipsoid or sphere - on a plane, can not take place without a change in shape. With a suitably chosen projection, however, you can keep the shape changes within certain limits, within the geographical area you are working with.

The earth model

For very small-scale maps, for example world maps, you use a spherical earth model. Usinga spherical model will provide simpler calculations. The result will not be as as accurate as when the ellipsoidal earth model is used. The errors are quite small and the accuracy is still not very high in world maps, and therefore the errors can be neglected. Using an ellispoidal earth model will result in more complicated formulas, where you will have to use series expansion.

Construction

The method for constructing the map projection can be divided into three main types in terms of:

• Shape of the projection surface: cylindrical, conical or azimuthal.
• Position of the projection surface: normal, transverse or oblique.

Cylindrical projection

A cylinder touches the equator (you then get a projection of normal type; image to the left), or along a mean meridian (the projection is then of transverse type; image to the right):

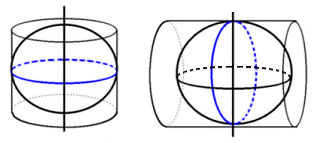
In addition, the cylinder can be differently oriented to get a so-called oblique projection aspect.

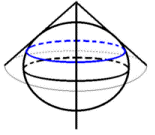
Conical projection

In a conical projection the globe is tangent to a cone, usually along a parallel circle.

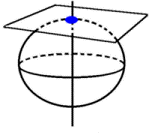
Azimuthal projection

In an azimuthal map projection, a plane touches the globe at a point. The normal type, when the tangent point is one of the poles, is usually called a polar aspect. The transverse type, if the tangent point is on the equator, is usually called an equatorial aspect. An oblique axis can also used. The image shows a polar aspect:

Perspective projection

A perspective projection can be constructed purely geometrically. Straight lines, projection beams, start from a point, the projection centre, through the points on the globe surface that are imaged, and extend until they intersect the projection surface in the image of the points.

As an example, we have the gnomonic projection (image below to the left) which is an azimuthal projection where the centre of the projection is the centre of the globe. The projection centre of the stereographic projection (image below in the middle) is the antipode of the tangent point. We also have the orthographic projection (image below to the right) where the projection centre is located at an infinite distance, i.e. the projection beams are parallel.

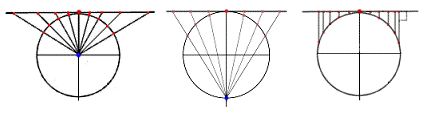
Mapping function

Most projections we use are not perspective. The mapping is made in a more complicated way and can be generally described as a mathematical function:

x = f _x ( j, l )
y = f _y ( j, l )

where j is geodetic latitude, l is geodetic longitude and x, y are plane coordinates in the projection plane.

In Sweden and some other countries the convention is that the x-axis in this context is directed to the north and the y-axis to the east. The rotation direction is positive clockwise, i.e. opposite to what is told in geometry textbooks, where the y-axis is directed upwards and the x-axis to the right. To avoid confusion, the axes are sometimes called 'Northing' and 'Easting', respectively. Lantmäteriet has also started to use 'Northing' and 'Easting' in Sweden for the various projections of SWEREF 99, still with a positive clockwise direction of rotation.

Important properties

By formulating conditions for the mapping function, you can give the projection different properties. The most important properties are:

Conformal

A conformal, or angle-preserving, projection means that an infinitely small figure is depicted without deformation, and that the magnification at a point is equal in all directions. Conformity cannot be combined with equivalence.

Equivalent

The surface of a figure on the globe surface is mapped onto the map plane as a figure with equal area. Equivalence cannot be combined with conformity.

Equidistant

This property can not apply generally, but only along certain lines, for example along the central meridian or a parallel circle.

In geodetic contexts, conformal projections are normally always used with an ellipsoidal earth model. A property of particular interest in conformal projections is meridian convergence.

Tissot's indicatrix

The so-called indicatrix, or Tissot's indicatrix, characterises the properties of a map projection. Tissot's indicatrix is the ellipse resulting from the projection of an elementary circle on the spherical surface. (An elementary circle is an infinitely small circle.)

In normal projections, the axes of the indicatrix are placed along the meridian and the parallel circle through the mapped point. If the radius of the elemental circle is chosen equal to one (1), then the magnifications h and k along the meridian and parallel circle, in the normal case, are equal to the lengths of the semi-axes of the indicatrix.

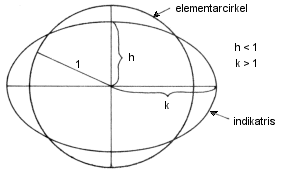
From the properties of the indicatrix, different types of projections can be identified:

• If h = k, the projection is conformal .
• If h * k = 1, the projection is equivalent.
• If h = 1 (k = 1), the projection is equidistand along the meridian (parallel circle).

The indicatrix also provides information about the angular distortion of the projection in the point. The maximum amount w is obtained from the formula:

sin (w) = | (k - h) / (k + h) |

Projection parameters

When specifying a projection, in addition to the general type, for example Gauss-Krüger, a number of parameters are specified.

The parameters of the earth ellipsoid must always be specified, but are often given indirectly of the geodetic datum or reference system used.

The other parameters that usually occur are:

• Central meridian; the centre meridian which is normally depicted as a vertical straight line and forms the axis of symmetry, and the natural x-axis of the planar system. The longitude (degrees, minutes, seconds) of the central meridian is given, usually relative to the international zero meridian of Greenwich.
• Standard parallels; are indicated for normal projections, and are parallel circles mapped to scale. A projection can have one or two standard parallels. The latitudes of these are given.
• Scale reduction factor; a number, less than or equal to 1, applied to the coordinates to redistribute the scale error in the projection. For example, in UTM, the scale reduction factor 0.9996 is used.
• The latitude of the tangent point; centre point for azimuthal projections. The latitude is specified.

A number of parameters are used to more or less arbitrarily redefine the origin of the projection system:

• False northing: x-addition (or negative values, for reductions)
• False easting: y-addition (or negative values, for reductions)

The following are not normally used in Sweden:

• Latitude of origin; here it is stated that the origin of the plane system should be located at a certain latitude.
• Longitude of origin; here it is stated that the origin of the planar system is to be located at a certain longitude. Is normally the same as the longitude of the central meridian.

Interactive services

• Coordinate transformations
• Calculate meridian convergence